지역성의 원리: 캐시가 빠른 이유

캐시는 지역성의 원리에 영향을 받습니다.

프로그래밍 언어는 대부분 반복, 재귀, 분기로 이루어져 있기에 “머지 않은 시간에 같은 메모리 영역에 접근”하거나 “한번 접근한 메모리 영역의 근처에 다시 접근”합니다.

시간지역성, Temporal Locality는 “머지 않은 시간에 같은 메모리 영역에 접근”,

공간지역성, Spacial Locality는 “한번 접근한 메모리 영역의 근처에 다시 접근” 한다는 개념입니다.

그러므로, 한번 접근했던 메모리 영역을 일정 단위만큼 뽑아 가까이 두면, 더 빨리 참조할 수 있을 것입니다.

이 때, 빠른 참조를 위해 일정량의 데이터를 저장하기 위한 장치를 “캐시”라고 하며,

캐시에서 정보를 저장하는 최소 단위를 “블록”이라고 합니다.

블록 크기는 캐시 성능에 많은 영향을 끼칩니다.

블록 크기가 커질수록 캐시 Hit Rate가 올라가지만, Miss Panatly역시 같이 커집니다.

이같은 캐시 성능평가와 관련된 내용은 아래에서 살펴봅니다.

캐시의 성능 평가

CPU 명령어가 특정 주소의 데이터를 요청했을 때, 이 데이터가 캐시에 있을 수도, 없을 수도 있습니다. 캐시에 데이터가 존재하거나 그렇지 않을 확률을 각각

“Hit Rate, Miss Rate” 라고 합니다.

캐시에 데이터가 존재한다면, 괜찮겠지만, 존재하지 않는다면 하위 레벨 캐시 또는 메모리로부터 데이터를 가져와야 합니다. 이 때, Cache Miss로 인해 데이터를 가져오는데 필요한 시간을

“Miss Panalty” 라고 합니다.

결론적으로, 평균 캐시 접근 성능은 아래와 같습니다.

Hit Rate * Hit Speed + Miss Rate * Miss Panalty

매핑방법: 어떻게 필요한 정보를 캐싱할까?

앞서 캐시는 블록 단위로 저장된다고 이야기했습니다.

운영체제의 페이징과 마찬가지로, 32bit (칩셋에 따라 64bit)의 가상 메모리주소를 나누어 캐시 블록을 식별합니다.

가상주소를 아래와 같이 나누어, 캐시 내에서 데이터 블록을 유일하게 식별합니다.

인덱스(Block Number): 캐시 블록을 특정하기 위해 사용하는 영역

태그(Tag): 캐시의 블록을 식별한 이후에 추가적인 식별을 위해 필요한 영역

변위(Offset) : 블록 내에서 Byte위치를 식별하기 위해 저장하며, 캐시 엔트리에는 저장되지 않습니다.

여러가지 매핑 방법과 캐시 엔트리 저장방법

글자 그대로는 이해하기 살짝 이해하기 힘들고, 어떻게 동작하는지 그림을 그려보면 알기 쉽습니다.

!!전제!!: 캐시의 성능과 가격을 고려해 결정됩니다. (계산의 용이함을 위해 작은 단위 사용)

32bit 컴퓨터로, 가상주소공간이 32bit로 표현됩니다.

캐시의 크기는 4KB입니다.

캐시 데이터블록 하나의 크기는 16Byte입니다.

1. Direct Mapping (직접 사상방법, 간편하지만 Hit Rate 낮다.)

인덱스 비트

그러르모, 캐시 엔트리 개수는, [ 캐시크기 / 캐시 엔트리 크기 ] = 4KB / 16 Byte = 2^12 / 2^4 = 2^8이므로, 인덱스는 8비트로 표현할 수 있습니다.

인덱스비트는 ‘캐시 내에서 엔트리 순서’의 의미를 가지므로, 인덱스 비트를 통해 O(1)의 시간으로 캐시 엔트리에 접근할 수 있습니다. Hash Table과 비슷하게 동작합니다.

Offset 비트

데이터블록 하나의 크기가 16Byte였습니다. 이는 간단히 4bit로 표현할 수 있습니다.

캐시 블록을 가져올 때, Offset을 통해 정확히 어떤 Byte를 가져와야 하는지 알 수 있습니다.

Tag비트

32bit에서 Offset과 Index를 표현하고 남는 부분인 주소공간 하위 부분입니다.

캐시 엔트리에 저장되어 인덱스로 식별한 캐시 블록이 실제로 필요한 데이터인지를 판별하는 중요한 역할을 합니다.

(인덱스가 같아도 태그가 모두 다르므로, & 연산을 통해 실제 원하는 데이터인지 확인할 수 있습니다)

가상 메모리 주소 ( 32 < - - - - - > 0 )

Tag(20bit)	Index ( 8bit 이상)	Byte Offet(4bit)

아래는 4바이트 데이터 블록을 갖는 캐시 엔트리입니다. 이같은 캐시 엔트리가 2^8개 존재하고, 가상 주소공간의 12bit ~ 4bit까지를 캐시 내의 인덱스로 사용합니다 .

valid(1bit)	Tag(20bit)	Data ( 16Byte)

Index bit와 Modulo를 통한 매핑

Index bit를, 캐시 내 블록 개수인 2^8이므로 8bit로 설정했지만, 이보다 더 큰 값을 설정할 수 있습니다.

캐시 내 블록 개수보다 더 큰, 가상주소공간의 Index에 대해서는

[ Index (Modulo) 캐시 내 블록 개수 ]를 통해 매핑할 수 있습니다.

인덱스 주소를 크게 가져가면, 캐시 엔트리 내에 저장해야 하는 태그비트를 줄일 수 있어 효율적입니다.

(Direct Mapping의 문제점)

Direct Mapping에서는 Tag비트가 다른 블록이더라도, Index bit가 같다면, 캐시메모리 내에서 고정된 위치에 할당됩니다.

따라서, Index가 같지만 Tag가 다른 두 블럭이 자주 사용된다면, 매번 Miss가 발생해, 캐시를 사용하지 않는것보다 성능이 나빠질 수 있습니다.

2. Fully Associative Mapping ( 연관 사상 방법 , 과도한 병렬처리 필요)

직접매핑 방법에서는 가상주소의 인덱스 필드 넘버에 따라 캐시 엔트리의 고정된 위치에 들어가야 했던 반면, 연관 매핑방법에서는 인덱스비트를 사용하지 않습니다.

(가상메모리 주소)

Tag ( 28 bit )	Offset (4 bit)

앞선 방법에서, 자주 사용되는 자리에서 캐시 미스가 발생하는 문제 없이, “실제로 자주 사용되는 블록”만 남길 수 있게 되었습니다.

그러나, “접근 방법”에 문제가 생깁니다.

직접연관에서는 가상주소에서 인덱스를 떼어서 캐시 엔트리 주소를 얻고, 테그 영역으로 실제 원하는 데이터인지 확인했습니다. 또는 Modulo를 이용한 방법으로, 인덱스가 Hash Table의 Key 역할을 했습니다.

연관 사상 방법에서는 태그를 비교하며 원하는 캐시 블록의 유무를 확인하기 위해 N to 1 Multiplexor를 사용해 병렬적으로 캐시에 접근합니다.

하지만, 병렬처리를위한 하드웨어는 캐시 크기가 커질수록 많은 비용을 지출합니다. ( 크기가 작은 캐시에서 주로 사용합니다 )

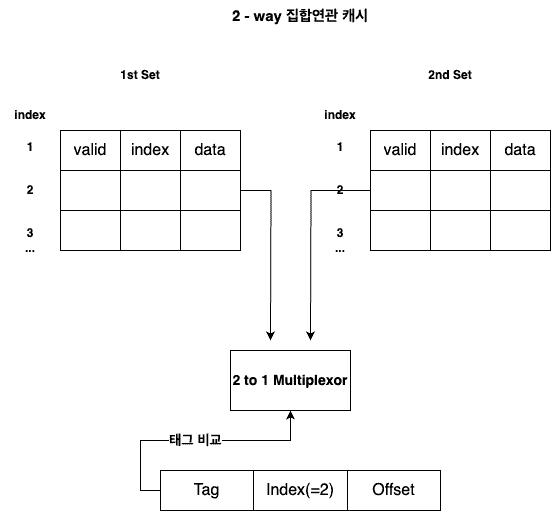
3. Set Associative Mapping (집합 연관 사상 방법, 절충안 - 적절한 Set크기 지정 필요)

집합연관 매핑에서는 N개의 집합이 존재하고, 집합 내에서 Index를 통해 접근할 수 있습니다.

만약 집합이 2개인 경우, (2-way set associative cache)

같은 인덱스를 갖는 데이터는 두 개의 집합에 들어갈 수 있습니다.

( 이해를 위한 사진으로, 실제로는 SET이 분리되어 저장되지 않습니다 )

집합연관 매핑에서 집합 개수가 늘어나는것을 “연관 정도가 늘어난다”라고 표현합니다.

연관정도가 올라갈 떄(집합의 수가 늘어날 때=N증가) 일어나는 일들

• 캐시 실패율이 줄어듭니다.
• 캐시 적중시간이 증가합니다.
• 병렬처리를 위한 Multiplexor비용이 늘어납니다.
• 캐시 블록 수가 동일하다면, 집합에 존재하는 블록 수가 줄어듭니다.
• 그에 따라, index비트가 줄고, Tag 비트가 늘어납니다. ⇒ 캐시 엔트리 크기 증가

기타

멀티레벨 캐시를 통해 지역성 원칙을 활용, 캐시 접근속도 향상

캐시 교체 방식

Reference

David A. Patterson , 컴퓨터 구조 및 설계 5th,